
Цель использования статистических методов - это сбор предварительной информации о данных для лучшего понимания контекста. Один из шагов в цикле анализа данных — это (лучшее) понимание данных. Описательная статистика помогает лучше понять контекст, и что важно - создает условие, когда начинаем задавать (правильные) вопросы и тем самым погружаемся в задачу. Например, почему у нас такая дорогая недвижимость - предположим, что в Варшаве 40 миллионов злотых (около 10 млн. евро). Может это ошибка? А может нет, просто экстремально большое значение.
В описательной статистике существуют разные техники, начиная от просмотра данных глазками (когда данных много, то обычно случайным образом выбираем 10-20 строк), графического представления (например, ящик с усами - более подробно будет в этом модуле), ну и конечно же различные показатели распределения (например среднее значение).
В описательной статистике существуют разные техники, начиная от просмотра данных глазками (когда данных много, то обычно случайным образом выбираем 10-20 строк), графического представления (например, ящик с усами - более подробно будет в этом модуле), ну и конечно же различные показатели распределения (например среднее значение).
Практическое введение в статистику
В 1 уроке 1 модуля узнаешь про:
✔️ среднее значение (арифметическое)
✔️ медиану, перцентиль (или процентиль), квартиль
✔️ выбросы или экстремальные значения (англ. `outliers`)
✔️ минимальные и максимальные значения
В следующих уроках 1 модуля:
- дисперсию и стандартное отклонение (не пугайся "умных" названий, они только кажутся сложными, на деле могут быть очень даже полезны)
- нормальное распределение и распределение с длинным хвостом
- правило трех сигм
- нормализация распределений с длинным хвостом: `log`, `boxcox`, `sqrt`
- количественные (непрерывные и дискретные) и категориальные (качественные и порядковые) переменные
- сумма и кумулятивная сумма
- визуализация: `box-plot`, `histogram`, `bar plot`.
- стандартная ошибка
- анализ нормального распределения (qq-plot)
- популяция, выборка и репрезентативная выборка
- систематическая ошибка выборки (англ. `selection bias`)
- и даже больше
Узнаешь, какие существуют подводные камни и на что следует обратить внимание, чтобы в реальной жизни делать правильные выводы на основе данных.
ПОШАГОВОЕ ВИДЕО ДЛЯ ПЕРВОГО УРОКА:
✔️ среднее значение (арифметическое)
✔️ медиану, перцентиль (или процентиль), квартиль
✔️ выбросы или экстремальные значения (англ. `outliers`)
✔️ минимальные и максимальные значения
В следующих уроках 1 модуля:
- дисперсию и стандартное отклонение (не пугайся "умных" названий, они только кажутся сложными, на деле могут быть очень даже полезны)
- нормальное распределение и распределение с длинным хвостом
- правило трех сигм
- нормализация распределений с длинным хвостом: `log`, `boxcox`, `sqrt`
- количественные (непрерывные и дискретные) и категориальные (качественные и порядковые) переменные
- сумма и кумулятивная сумма
- визуализация: `box-plot`, `histogram`, `bar plot`.
- стандартная ошибка
- анализ нормального распределения (qq-plot)
- популяция, выборка и репрезентативная выборка
- систематическая ошибка выборки (англ. `selection bias`)
- и даже больше
Узнаешь, какие существуют подводные камни и на что следует обратить внимание, чтобы в реальной жизни делать правильные выводы на основе данных.
ПОШАГОВОЕ ВИДЕО ДЛЯ ПЕРВОГО УРОКА:
Урок 1
Цитата и факты
Существует три типа лжи: ложь, ужасная ложь, статистика
Существует три типа лжи: ложь, ужасная ложь, статистика
Книга - Как лгать при помощи статистики (Статистически самая популярная книга в статистике)
Политики также часто любят использовать статистику для достижения своих целей.
---
Звучит странно, тем более что мы хотим начать изучать статистику, правда? Позволь мне сразу сказать, что мой авторский курс имеет благие намерения и призван сделать этот мир лучше для многих людей! Это важное уточнение, мотивация и стремление.
Я хочу показать Тебе, как статистика может помочь в извлечении ценности из данных (кстати, именно этим мы занимаемся в DataWorkshop - извлечением ценности из данных).
---
Что такое статистика?
Существуют различные умные определения, но давай начнем с грубого и "по-своему".
Статистика - это своего рода искусственное творение - наука, которая была создана людьми для того, чтобы облегчить работу с данными, например, делать выводы, опираясь на данные.
Важный вывод: статистика это инструмент, который используем чтобы более качественно и эффективно работать с данными.
---
Звучит странно, тем более что мы хотим начать изучать статистику, правда? Позволь мне сразу сказать, что мой авторский курс имеет благие намерения и призван сделать этот мир лучше для многих людей! Это важное уточнение, мотивация и стремление.
Я хочу показать Тебе, как статистика может помочь в извлечении ценности из данных (кстати, именно этим мы занимаемся в DataWorkshop - извлечением ценности из данных).
---
Что такое статистика?
Существуют различные умные определения, но давай начнем с грубого и "по-своему".
Статистика - это своего рода искусственное творение - наука, которая была создана людьми для того, чтобы облегчить работу с данными, например, делать выводы, опираясь на данные.
Важный вывод: статистика это инструмент, который используем чтобы более качественно и эффективно работать с данными.
Статистика помогает извлекать ценность из данных (например, задавать правильные вопросы, проверять гипотезы, принимать правильные решения и т.д.). Давай прямо с этого момента смотреть на статистику, именно с точки зрения практического инструмента.
При случае подскажу, если же начинаешь изучать статистику с классической стороны (например, в университете), то статистически, т.е. скорее всего, придешь в ужас от количества формул, различных названий и формальностей. У меня была статистика в университете, и она мне очень не нравилась. Знаешь, почему? Мой преподаватель не был практикующим специалистом и объяснял все абстрактно. Как результат я не любил статистику, она мне казалась оторванной от жизни... и вот теперь я учу Тебя. А знаешь почему?
Я вернулся к статистике, но с другой стороны. Я с детства интересовался анализом данных или различными явлениями (я всегда что-то рассматривал, обдумывал или прогнозировал по-своему), это означало, что я начал придумывать свои собственные различные способы анализа и действий. В какой-то момент я понял, что мне нужно вернуться к статистике и посмотреть на нее под другим углом, не тем, что показывали в университете. Ведь там уже есть много чего готового, просто подача часто сильно абстрактная, но это не меняет сути.
Цель которую себе поставил тогда - это смотреть на статистику с преимущественно практической точки зрения и использовать ее для конкретных целей и задач, а не с абстрактной точки зрения [какие-то формулы, оторванные от контекста]. И это дало свои результаты.
И именно этим опытом, подходом и перспективой хочу поделится с Тобой (кстати, т.к. я самоучка приготовься что будет иначе, чем обычно. Моей целью является донести практическую мысль, объясняя на пальцах, котиках или еще как-то).
Статистика может быть полезна для извлечения ценностей из данных. Важно лишь понять, как применять это на практике. Я надеюсь и верю, что изучение статистики через истории или различные аналогии поможет Тебе лучше запомнить ее с фундаментальной стороны, а позже Ты также лучше усвоишь теоретические нюансы, если захочешь (т.е. мой подход вовсе не вычеркивает академические формулы, наоборот, дает больший шанс начать работать с данными).
Ну что, начинаем!
Я вернулся к статистике, но с другой стороны. Я с детства интересовался анализом данных или различными явлениями (я всегда что-то рассматривал, обдумывал или прогнозировал по-своему), это означало, что я начал придумывать свои собственные различные способы анализа и действий. В какой-то момент я понял, что мне нужно вернуться к статистике и посмотреть на нее под другим углом, не тем, что показывали в университете. Ведь там уже есть много чего готового, просто подача часто сильно абстрактная, но это не меняет сути.
Цель которую себе поставил тогда - это смотреть на статистику с преимущественно практической точки зрения и использовать ее для конкретных целей и задач, а не с абстрактной точки зрения [какие-то формулы, оторванные от контекста]. И это дало свои результаты.
И именно этим опытом, подходом и перспективой хочу поделится с Тобой (кстати, т.к. я самоучка приготовься что будет иначе, чем обычно. Моей целью является донести практическую мысль, объясняя на пальцах, котиках или еще как-то).
Статистика может быть полезна для извлечения ценностей из данных. Важно лишь понять, как применять это на практике. Я надеюсь и верю, что изучение статистики через истории или различные аналогии поможет Тебе лучше запомнить ее с фундаментальной стороны, а позже Ты также лучше усвоишь теоретические нюансы, если захочешь (т.е. мой подход вовсе не вычеркивает академические формулы, наоборот, дает больший шанс начать работать с данными).
Ну что, начинаем!
Коты и среднее значение
С чего начать? Как насчет кода или хотя бы кота? На самом деле, код также появится через некоторое время, но давай начнем с котов. Представь себе, что есть бабушка, которая любит котов (или коты любят бабушку, это уже не так важно), и у нее есть, например, пять котов. У каждого кота свой рост. Предположим, что рост кота измеряется от лап до ушей (мы будем считать так, кто нам может запретить, хотя можно считать и по-другому) - красная стрелка (рисунок ниже) показывает рост наших котов.
Наша задача - (пока визуально) сказать, какой у них средний рост (смотри на рисунке ниже).
С чего начать? Как насчет кода или хотя бы кота? На самом деле, код также появится через некоторое время, но давай начнем с котов. Представь себе, что есть бабушка, которая любит котов (или коты любят бабушку, это уже не так важно), и у нее есть, например, пять котов. У каждого кота свой рост. Предположим, что рост кота измеряется от лап до ушей (мы будем считать так, кто нам может запретить, хотя можно считать и по-другому) - красная стрелка (рисунок ниже) показывает рост наших котов.
Наша задача - (пока визуально) сказать, какой у них средний рост (смотри на рисунке ниже).

Видно, что черный кот самый высокий, первый - самый низкий, но также видно, что коты довольно одинаковы по росту. Назовем это средним ростом котов. Очевидно, что коты меньше людей, но больше муравьев, верно? С другой стороны, какой средний рост котов?
Если у Тебя есть кошка (или кот), можешь измерить прямо сейчас :)
В данном случае предположим, что у нас рост котов от 32 см до 38 см.
Как видно на рисунке (синяя линия), примерно так можно визуально определить средний рост у котов (что-то около 35 см).
Обрати внимание, что визуальная интерпретация важна, она стимулирует воображение (образы, истории).
Старайся думать о проблеме, которую решаешь, как можно более реалистично, а не просто смотря только на таблицы данных. Тогда, как правило, будет легче справиться с извлечением ценности из данных (а именно к этому стремимся).
Теперь давай определим проблему более точно, чем просто визуально. Пришло время для кода, который поможет котам вычислить средний рост.
Если впервые столкнешься с кодом (будем использовать язык программирования Python или питон), то не пугайся, когда-то это должно было случиться, Ты в надежных руках.
Импортируем библиотеки
Библиотеки - это готовый, ранее написанный код. Использовать библиотеки - это очень популярная и эффективная практика у многих IT специалистов (сильно упрощает жизнь).
Мы будем довольно часто использовать библиотеку `numpy`, которая оптимизирована для подсчета больших наборов данных.
Если у Тебя есть кошка (или кот), можешь измерить прямо сейчас :)
В данном случае предположим, что у нас рост котов от 32 см до 38 см.
Как видно на рисунке (синяя линия), примерно так можно визуально определить средний рост у котов (что-то около 35 см).
Обрати внимание, что визуальная интерпретация важна, она стимулирует воображение (образы, истории).
Старайся думать о проблеме, которую решаешь, как можно более реалистично, а не просто смотря только на таблицы данных. Тогда, как правило, будет легче справиться с извлечением ценности из данных (а именно к этому стремимся).
Теперь давай определим проблему более точно, чем просто визуально. Пришло время для кода, который поможет котам вычислить средний рост.
Если впервые столкнешься с кодом (будем использовать язык программирования Python или питон), то не пугайся, когда-то это должно было случиться, Ты в надежных руках.
Импортируем библиотеки
Библиотеки - это готовый, ранее написанный код. Использовать библиотеки - это очень популярная и эффективная практика у многих IT специалистов (сильно упрощает жизнь).
Мы будем довольно часто использовать библиотеку `numpy`, которая оптимизирована для подсчета больших наборов данных.
import numpy as np
import pandas as pd
pd.set_option('display.float_format', lambda x: '%.3f' % x)
Предположим, что рост наших котов (по очереди с рисунка): 32см, 33см, 35см, 38см и 35см. Давай присвоим эти значения в виде списка переменной `height_cats`.
Код
height_cats = [32, 33, 35, 38, 35]
Давай сначала рассчитаем "в ручном режиме" среднее значение. Для этого нужно взять сумму роста всех котов и разделить ее на количество котов.
Код
(32 + 33 + 35 + 38 + 35) / 5
Результат: 34.6
Средний рост кота составил 34,6 см. Для простоты в дальнейшем мы будем использовать функцию `np.mean()`, которая занимает меньше места и лучше считает среднее значение (даже для миллиона или миллиарда значений).
Код
np.mean(height_cats)
Результат: 34.6
Как можно увидеть, результат тот же.
Ты уже знаешь, как вычислить среднее значение. Точнее говоря, это среднее арифметическое или более научно ожидаемое значение, хотя оно рассчитывается более сложным способом, но с нашими котами получается то же самое.
Обычно среднее записывается как x (или какая-то другая переменная) с "черточкой", это выглядит, например, так x (добавлю, что это среднее по выборке, что это за "выборка" и чем она отличается от популяции - об этом будет рассказано в следующих уроках в этом модуле).
Среднее значение очень популярно в различных контекстах, например, средняя оценка в школе, средняя цена недвижимости на рынке или среднее значение по стране (зарплата). Средний показатель прост для понимания, но может заставить нас сделать неправильные выводы, потому что мы интерпретируем его не так, как следовало бы.
Средняя зарплата
Чтобы лучше понять это, давай рассмотрим пример, непосредственно связанный с деньгами. Обычно такие примеры лучше "заходят" и запоминаются.
Предположим, у нас есть компания из 10 человек (9 сотрудников и один "большой босс"). Работники (т.е. 9 человек) зарабатывают по 1000 евро и "большой босс" зарабатывает 41 000 евро. Тогда у нас затраты компании на зарплаты составляют 50 000 евро. Если разделить 50 000 евро на 10 людей (именно столько человек работает в компании, включая "большого босса"), то получится, что в среднем в этой компании человек зарабатывает 5000 евро. Что может стать большим сюрпризом для 9 сотрудников этой компании, если они узнают об этом .
Ты уже знаешь, как вычислить среднее значение. Точнее говоря, это среднее арифметическое или более научно ожидаемое значение, хотя оно рассчитывается более сложным способом, но с нашими котами получается то же самое.
Обычно среднее записывается как x (или какая-то другая переменная) с "черточкой", это выглядит, например, так x (добавлю, что это среднее по выборке, что это за "выборка" и чем она отличается от популяции - об этом будет рассказано в следующих уроках в этом модуле).
Среднее значение очень популярно в различных контекстах, например, средняя оценка в школе, средняя цена недвижимости на рынке или среднее значение по стране (зарплата). Средний показатель прост для понимания, но может заставить нас сделать неправильные выводы, потому что мы интерпретируем его не так, как следовало бы.
Средняя зарплата
Чтобы лучше понять это, давай рассмотрим пример, непосредственно связанный с деньгами. Обычно такие примеры лучше "заходят" и запоминаются.
Предположим, у нас есть компания из 10 человек (9 сотрудников и один "большой босс"). Работники (т.е. 9 человек) зарабатывают по 1000 евро и "большой босс" зарабатывает 41 000 евро. Тогда у нас затраты компании на зарплаты составляют 50 000 евро. Если разделить 50 000 евро на 10 людей (именно столько человек работает в компании, включая "большого босса"), то получится, что в среднем в этой компании человек зарабатывает 5000 евро. Что может стать большим сюрпризом для 9 сотрудников этой компании, если они узнают об этом .
_
_

Давай также проверим, посчитав это с помощью кода. Сначала создадим переменную `salaries`.
Подсказка:
Я использую трюк из Pythonа, чтобы не писать 9 раз 1000 (пустая трата времени, пусть компьютер нам поможет ????). Я делаю это так `[1000]*9`, в результате мы получаем список, который содержит 9 раз по 1000, так что будет вот такой список `[1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000]`. Это довольно удобно (и стоит запомнить). Затем мы приклеиваем к этому списку еще одно значение 41 000 (т.е. зарплату "большого босса").
В результате у нас появилась переменная `salaries`, которая состоит из 10 зарплат (т.е. зарплаты 10 человек, работающих в компании).
Подсказка:
Я использую трюк из Pythonа, чтобы не писать 9 раз 1000 (пустая трата времени, пусть компьютер нам поможет ????). Я делаю это так `[1000]*9`, в результате мы получаем список, который содержит 9 раз по 1000, так что будет вот такой список `[1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000]`. Это довольно удобно (и стоит запомнить). Затем мы приклеиваем к этому списку еще одно значение 41 000 (т.е. зарплату "большого босса").
В результате у нас появилась переменная `salaries`, которая состоит из 10 зарплат (т.е. зарплаты 10 человек, работающих в компании).
Код
salaries = [1000] * 9 + [41000]
salaries
Результат: [1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 41000]
Теперь вычислим среднее (арифметическое) значение, используя `np.mean`
Код
np.mean(salaries)
Результат: 5000.0
Как видишь, код показал то же самое (как мы и ожидали, потому что выше мы уже посчитали "по-быстрому"). В итоге мы получили, что средний заработок в компании составляет 5 000 евро.
Кстати, одна из причина почему среднюю зарплату измеряют в качестве средней величины, но по факту эта величина несколько искажает реальное положение дел. Как мы можем измерить (например, зарплату) по-другому, чтобы лучше отразить реальность (ведь в нашем примере 9 из 10 человек зарабатывают 1000 евро это в 5 раз меньше чем среднее 5000 евро)
Давай сделаем очередной вывод.
Среднее значение не всегда является лучшим способом описания группы (например, средняя зарплата или средний балл).
Давай покажу еще одну аналогию, которая должна еще больше проиллюстрировать и закрепить проблему того, почему следует быть очень осторожным, делая выводы на основе среднего значения.
Средняя температура тела по больнице 36,6 C
Как известно, нормальная температура тела здорового человека в среднем должна составлять около 36,6 С.
Для примера, у нас есть информация - какая средняя температура у пациентов в больнице - и, например, она как раз вышла 36.6 С. Можно сделать вывод - все хорошо. Все пациенты здоровы и могут быть отпущены домой. Но! Есть и другой сценарий (и даже может быть более реалистичен в этому случае).
Предположим, что у нас в больнице находятся пять пациентов с температурой тела 42,6 C и пять пациентов с температурой тела 30,6 C. В данном случае среднее значение температуры тела у пациентов составляет 36,6 C. Если смотреть только на среднее значение - как-будто идеальная ситуация. Только в действительности ситуация критическая и людей нужно спасать!
Давай проверим еще с помощью кода. Создадим новую переменную `temperatures` и вычислим среднее значение с помощью `np.mean`.
Кстати, одна из причина почему среднюю зарплату измеряют в качестве средней величины, но по факту эта величина несколько искажает реальное положение дел. Как мы можем измерить (например, зарплату) по-другому, чтобы лучше отразить реальность (ведь в нашем примере 9 из 10 человек зарабатывают 1000 евро это в 5 раз меньше чем среднее 5000 евро)
Давай сделаем очередной вывод.
Среднее значение не всегда является лучшим способом описания группы (например, средняя зарплата или средний балл).
Давай покажу еще одну аналогию, которая должна еще больше проиллюстрировать и закрепить проблему того, почему следует быть очень осторожным, делая выводы на основе среднего значения.
Средняя температура тела по больнице 36,6 C
Как известно, нормальная температура тела здорового человека в среднем должна составлять около 36,6 С.
Для примера, у нас есть информация - какая средняя температура у пациентов в больнице - и, например, она как раз вышла 36.6 С. Можно сделать вывод - все хорошо. Все пациенты здоровы и могут быть отпущены домой. Но! Есть и другой сценарий (и даже может быть более реалистичен в этому случае).
Предположим, что у нас в больнице находятся пять пациентов с температурой тела 42,6 C и пять пациентов с температурой тела 30,6 C. В данном случае среднее значение температуры тела у пациентов составляет 36,6 C. Если смотреть только на среднее значение - как-будто идеальная ситуация. Только в действительности ситуация критическая и людей нужно спасать!
Давай проверим еще с помощью кода. Создадим новую переменную `temperatures` и вычислим среднее значение с помощью `np.mean`.
Код
temperatures = [42.6] * 5 + [30.6]*5
np.mean(temperatures)
Результат: 36.60000000000001
Может показаться, что этот пример довольно банален, но поверь - многие компании имеют похожие метрики и кажется, что все хорошо, но ситуация прямо противоположная. Постарайся использовать этот пример, когда будешь смотреть на данные и понимать, что эти данные означают (возможно это просто "средняя по больнице" и нужно погрузиться в детали). Среднее значение, это один из примеров, насколько осторожно нужно делать выводы (дальше будет больше).
Откуда берется эта проблема?
Сейчас я назову две фундаментальные причины, на которые стоит обратить свое внимание!
Первая, очень важная (хотя о ней почти никогда не говорят). Смотри, в данном случае у нас ситуация, когда мы передаем список значений (например, температуру, или цену недвижимости, или средний балл в школе), и этот список может содержать 10 значений, или 100, или даже миллионы значений, но в результате мы получаем одно значение (которое пытается "описать" или "охарактеризовать" тысячи или миллионы других значений)! Это означает, что мы сжимаем информацию из многих значений в одно значение. Более того, мы не можем однозначно восстановить список исходных значений на основании среднего значения (это так называемое сжатие информации с потерями, то есть сжатие информации в одном направлении). Обрати на это особое внимание, потому что далее мы будем говорить о других агрегатных функциях (не только о среднем значении), и все они имеют ту же проблему. Средняя по зарплате в стране описывает зарплаты миллионы людей. Очень сложно найти такое число, которое ёмко опишет ситуацию обо всей стране.
Подумай об этом так. На вход "приходит" список значений (и это могут быть тысячи значений или даже миллионы, или миллиарды значений), но в результате всегда возвращается только одно значение. Что по определению уже усложняет ситуацию, поскольку нам приходится описывать целую группу значений (например, миллионы значений), используя только одно значение (число). Очень трудно выразить мысль только одним значением (или одним словом), не так ли? Здесь то же самое.
Второй момент - среднее значение довольно чувствительно к выбросам. Выброс (англ. `outliers`) - это экстремальное значение, которое значительно отличается от других (слишком маленькое или слишком большое). В примере с зарплатой зарплата "большого босса" составляло €41 000, и это значительно отличалось от зарплаты других сотрудников (€1 000).
Выбросы могут вызвать большие проблемы при интерпретации данных, и, как уже упоминалось среднее очень чувствительно на выбросы (иными словами, выбросы "искажают среднюю"). Почему? Потому что среднее значение учитывает все значения (т.е. мы находим сначала сумму всех значений, также учитывая аномалию [т.е. выбросы]), а затем делим на количество значений. Более того, в теории обычно мало внимания уделяется выбросам, но на практике они почти всегда появляются и почти всегда усложняют жизнь (по крайней мере, новичкам). С другой стороны, чем раньше узнаешь о возможных трудностях, с которыми можешь столкнуться в реальной жизни, тем быстрее сможешь начать работать с ними и повысить вероятность того, что сможешь с этим справиться.
Откуда берется эта проблема?
Сейчас я назову две фундаментальные причины, на которые стоит обратить свое внимание!
Первая, очень важная (хотя о ней почти никогда не говорят). Смотри, в данном случае у нас ситуация, когда мы передаем список значений (например, температуру, или цену недвижимости, или средний балл в школе), и этот список может содержать 10 значений, или 100, или даже миллионы значений, но в результате мы получаем одно значение (которое пытается "описать" или "охарактеризовать" тысячи или миллионы других значений)! Это означает, что мы сжимаем информацию из многих значений в одно значение. Более того, мы не можем однозначно восстановить список исходных значений на основании среднего значения (это так называемое сжатие информации с потерями, то есть сжатие информации в одном направлении). Обрати на это особое внимание, потому что далее мы будем говорить о других агрегатных функциях (не только о среднем значении), и все они имеют ту же проблему. Средняя по зарплате в стране описывает зарплаты миллионы людей. Очень сложно найти такое число, которое ёмко опишет ситуацию обо всей стране.
Подумай об этом так. На вход "приходит" список значений (и это могут быть тысячи значений или даже миллионы, или миллиарды значений), но в результате всегда возвращается только одно значение. Что по определению уже усложняет ситуацию, поскольку нам приходится описывать целую группу значений (например, миллионы значений), используя только одно значение (число). Очень трудно выразить мысль только одним значением (или одним словом), не так ли? Здесь то же самое.
Второй момент - среднее значение довольно чувствительно к выбросам. Выброс (англ. `outliers`) - это экстремальное значение, которое значительно отличается от других (слишком маленькое или слишком большое). В примере с зарплатой зарплата "большого босса" составляло €41 000, и это значительно отличалось от зарплаты других сотрудников (€1 000).
Выбросы могут вызвать большие проблемы при интерпретации данных, и, как уже упоминалось среднее очень чувствительно на выбросы (иными словами, выбросы "искажают среднюю"). Почему? Потому что среднее значение учитывает все значения (т.е. мы находим сначала сумму всех значений, также учитывая аномалию [т.е. выбросы]), а затем делим на количество значений. Более того, в теории обычно мало внимания уделяется выбросам, но на практике они почти всегда появляются и почти всегда усложняют жизнь (по крайней мере, новичкам). С другой стороны, чем раньше узнаешь о возможных трудностях, с которыми можешь столкнуться в реальной жизни, тем быстрее сможешь начать работать с ними и повысить вероятность того, что сможешь с этим справиться.
Медиана
Вернемся к примеру компании из 10 человек. Средняя была 5000 евро. Что плохо описывает ситуацию. Как мы еще можем описать группу, чтобы она была лучшего качества, чем "среднее по больнице"? Это можно сделать разными способами. Давай познакомимся с медианой, которая, безусловно, менее популярна, чем среднее значение, но сама идея очень проста, а также полезна (особенно в реальной жизни).
Чтобы найти медиану, мы должны выполнить три действия.
Давай сразу разберем пример.
Медиана - четное количество значений
Давай рассмотрим это на примере и пройдем шаг за шагом.
Вернемся к примеру компании из 10 человек. Средняя была 5000 евро. Что плохо описывает ситуацию. Как мы еще можем описать группу, чтобы она была лучшего качества, чем "среднее по больнице"? Это можно сделать разными способами. Давай познакомимся с медианой, которая, безусловно, менее популярна, чем среднее значение, но сама идея очень проста, а также полезна (особенно в реальной жизни).
Чтобы найти медиану, мы должны выполнить три действия.
- 1. Отсортировать значения в порядке возрастания, то есть в начале наименьшее значение, в конце наибольшее (в нашем примере отсортировать зарплаты от самой маленькой до самой большой).
- 2. Найти, где находится середина (среди всех значений).
- 3. Найти медиану, но нужно быть осторожными! Возможно как минимум два сценария: если у нас нечетное число значений (более простой случай), мы возвращаем центральное значение (посередине), если у нас четное число значений (более сложный и наш случай), мы берем два значения - одно сразу до середины и другое сразу после середины и находим среднее значение этой пары (посмотри на рисунок ниже).
Давай сразу разберем пример.
Медиана - четное количество значений
Давай рассмотрим это на примере и пройдем шаг за шагом.

1. Сначала мы сортируем значения в порядке возрастания. В нашем случае 9 сотрудников зарабатывают €1 000, а "большой босс" зарабатывает €41000. Поэтому он определенно должен находиться на крайней позиции (справа, потому что у него самая высокая зарплата из всех).
2. Середина в данном случае находится между значениями 5 и 6 (потому что в компании работает четное количество людей - 10 человек).
3. Затем мы переходим к немного более сложному сценарию, берем одно значение слева от центра и одно значение справа от центра (в данном случае это сотрудник 5 и сотрудник 6), у нас есть два значения (т.е. пара), и мы находим среднее этой пары. В нашем случае оба сотрудника имеют зарплату €1000, поэтому медианное значение также будет равно €1000 (т.е. `(1000 + 1000) / 2 = 1000`).
Таким образом, мы нашли медиану (в дальнейшем мы постараемся лучше это интерпретировать).
Медиана - нечетное количество значений
Рассмотрим более простой случай, когда у нас нечетное количество значений (предположим, что в компании 9 человек, 8 из которых зарабатывают 1000 злотых, а один - 41 000 злотых). В данном случае средний элемент - это пятый сотрудник. Поэтому мы просто возвращаем значение пятого элемента (пятого сотрудника), в данном случае это 1000.
2. Середина в данном случае находится между значениями 5 и 6 (потому что в компании работает четное количество людей - 10 человек).
3. Затем мы переходим к немного более сложному сценарию, берем одно значение слева от центра и одно значение справа от центра (в данном случае это сотрудник 5 и сотрудник 6), у нас есть два значения (т.е. пара), и мы находим среднее этой пары. В нашем случае оба сотрудника имеют зарплату €1000, поэтому медианное значение также будет равно €1000 (т.е. `(1000 + 1000) / 2 = 1000`).
Таким образом, мы нашли медиану (в дальнейшем мы постараемся лучше это интерпретировать).
Медиана - нечетное количество значений
Рассмотрим более простой случай, когда у нас нечетное количество значений (предположим, что в компании 9 человек, 8 из которых зарабатывают 1000 злотых, а один - 41 000 злотых). В данном случае средний элемент - это пятый сотрудник. Поэтому мы просто возвращаем значение пятого элемента (пятого сотрудника), в данном случае это 1000.

Теперь также проверим в коде, сначала для четного числа (10 человек в компании) создадим переменную `salaries_even` и затем с помощью функции `np.median` найдем медиану.
Код
salaries_even = [1000] * 9 + [41000]
np.median(salaries_even)
Результат: 1000.0
Теперь сделай то же самое, но для нечетного числа (например, 9 человек в компании). Давай создадим новую переменную `salaries_odd` и затем воспользуемся функцией `np.median` для нахождения медианы.
Код
salaries_odd = [1000] * 8 + [41000]
np.median(salaries_odd)
Результат: 1000.0
Как можно увидеть, в обоих случаях (как и выше визуально), нам вернулась 1000.
Больше примеров
Давай немного изменим этот пример (точнее, значения), чтобы увидеть разницу в случае четного и нечетного количества работников, а затем перейдем к интерпретации.
Больше примеров
Давай немного изменим этот пример (точнее, значения), чтобы увидеть разницу в случае четного и нечетного количества работников, а затем перейдем к интерпретации.

Код
salaries_even_two = [1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 41000]
np.median(salaries_even_two)
Результат: 5500.0
Как видишь, в данном случае медиана равна 5500, поскольку у нас четное количество значений (более сложный случай). Итак, сначала мы находим середину (в данном случае между сотрудниками 5 и 6), затем берем эту "пару", поэтому в данном случае у нас это сотрудник 5 (с зарплатой 5000 евро) и сотрудник 6 (с зарплатой 6000 евро). Медианное значение зарплаты этих работников составляет €5500, поэтому (5000 + 6000) / 2 = €5500.
Уже знаешь, что такое медиана (обрати внимание на парадокс, что в этом случае мы используем среднее значение для нахождения медианы, но среднее используем только для "центральной пары").
А давай еще проверим, как изменилось среднее значение для всех сотрудников этой компании (с новой конфигурацией заработной платы).
Уже знаешь, что такое медиана (обрати внимание на парадокс, что в этом случае мы используем среднее значение для нахождения медианы, но среднее используем только для "центральной пары").
А давай еще проверим, как изменилось среднее значение для всех сотрудников этой компании (с новой конфигурацией заработной платы).
Код
np.mean(salaries_even_two)
Результат: 8600.0
В данном случае среднее значение составляет 8600 евро (что все еще достаточно много для большинства людей в компании). Потому что на самом деле только два человека зарабатывают столько или больше (всем известный "большой босс" и в данном случае еще работник №9).
Давай еще сделаем что-то похожее, но только для нечетного числа людей в компании (чтобы увидеть, что медиана будет отличаться от четного случая).
Давай еще сделаем что-то похожее, но только для нечетного числа людей в компании (чтобы увидеть, что медиана будет отличаться от четного случая).

Код
salaries_odd_two = [1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 41000]
np.median(salaries_odd_two)
Результат: 5000.0
Как вы видишь, в данном случае медиана равна €5000 (для четного, т.е. 10 сотрудников медиана вышла €5500), потому что медиана приходится как раз на пятого сотрудника. Получается четыре слева, четыре справа и пятый - "центральный". Здесь не нужно "городить огород" со средним для пары.
Давай также найдем среднее значение для этого примера (9 сотрудников, не 10).
Давай также найдем среднее значение для этого примера (9 сотрудников, не 10).
Код
np.mean(salaries_odd_two)
Результат: 8555.555555555555
Среднее значение составляет 8555,56 евро, как и в прошлый раз, это все еще слишком много для большинства. Потому что все, кроме "большого босса", зарабатывают меньше 8555,56 евро.
Уже в этом варианте видно, что медиана может быть рассчитана , как минимум, двумя способами: для четного и нечетного числа значений. Стоит визуально еще раз взглянуть и тоже понять, что это усложнение для четного числа вполне естественно. Среднего элемента просто не существует. Конкретно в этом случае у нас есть пять работников перед серединой и пять после, нет непосредственно одного работника ("центрального"), который находится в середине. Таким образом, получается такая "смесь" (раз нет центрального, то будет центральная "пара"). Подумай об этом так: хорошо, поскольку нет среднего элемента, давай возьмем элемент с левой стороны и элемент с правой стороны, таким образом мы получим два значения (центральная пара), но медиана должна возвращать одно значение, а не два. Хорошо... тогда, чтобы "сжать" два значения до одного давай найдем среднее этой пары. Когда думаешь об этом таким образом, то такой подход становится более естественным.
Теперь перейдем к интерпретации медианы, к тому, как следует понимать медиану так по-человечески, а также какие преимущества и недостатки она имеет по сравнению со средним значением.
Уже в этом варианте видно, что медиана может быть рассчитана , как минимум, двумя способами: для четного и нечетного числа значений. Стоит визуально еще раз взглянуть и тоже понять, что это усложнение для четного числа вполне естественно. Среднего элемента просто не существует. Конкретно в этом случае у нас есть пять работников перед серединой и пять после, нет непосредственно одного работника ("центрального"), который находится в середине. Таким образом, получается такая "смесь" (раз нет центрального, то будет центральная "пара"). Подумай об этом так: хорошо, поскольку нет среднего элемента, давай возьмем элемент с левой стороны и элемент с правой стороны, таким образом мы получим два значения (центральная пара), но медиана должна возвращать одно значение, а не два. Хорошо... тогда, чтобы "сжать" два значения до одного давай найдем среднее этой пары. Когда думаешь об этом таким образом, то такой подход становится более естественным.
Теперь перейдем к интерпретации медианы, к тому, как следует понимать медиану так по-человечески, а также какие преимущества и недостатки она имеет по сравнению со средним значением.
Интерпретация медианы
В случае медианы мы обычно можем более надежно описать группу в виде одного значения. Довольно часто в практических данных встречаются так называемые выбросы, поэтому если мы смотрим только на среднее значение, оно обычно будет завышено или занижено (при условии, что "выброс" значительно больше (меньше) большинства значений - это очень распространенный случай, который можно встретить на практике).
Медиана, означает, что половина значений меньше или равно медиане (и наоборот). Так что, по-человечески, половина людей в компании зарабатывают 1000 евро (или меньше), а другая половина людей в компании зарабатывают 1000 евро или больше. Я думаю, Ты согласишься, что такое описание более полезно, чем сказать, что средняя зарплата в компании составляет 5000 евро.
В случае медианы мы обычно можем более надежно описать группу в виде одного значения. Довольно часто в практических данных встречаются так называемые выбросы, поэтому если мы смотрим только на среднее значение, оно обычно будет завышено или занижено (при условии, что "выброс" значительно больше (меньше) большинства значений - это очень распространенный случай, который можно встретить на практике).
Медиана, означает, что половина значений меньше или равно медиане (и наоборот). Так что, по-человечески, половина людей в компании зарабатывают 1000 евро (или меньше), а другая половина людей в компании зарабатывают 1000 евро или больше. Я думаю, Ты согласишься, что такое описание более полезно, чем сказать, что средняя зарплата в компании составляет 5000 евро.

В модифицированном примере у нас была медиана 5500 евро. Это означает, что половина работников зарабатывает 5500 евро (или меньше), а другая половина - 5550 евро или больше. Опять же, это описание более полезно (и ёмко) для большинства, чтобы правильнее интерпретировать группу значений, чем сказать, что средний заработок в компании составляет 8600 евро. Что думаешь по этому поводу?

Среднее значение vs медиана
Чтобы найти среднее значение, мы используем все значения (например, все зарплаты сотрудников). Для медианы необходимо только центральное значение (возможно, центральная пара - значения, непосредственно перед серединой и непосредственно после середины).
Среднее значение очень чувствительно к выбросам (потому что суммирует все значения). Поскольку медиана не учитывает все значения, она гораздо более устойчива к выбросам (в центре "собираются середнячки", а не выбросы).
Чтобы найти среднее значение, мы используем все значения (например, все зарплаты сотрудников). Для медианы необходимо только центральное значение (возможно, центральная пара - значения, непосредственно перед серединой и непосредственно после середины).
Среднее значение очень чувствительно к выбросам (потому что суммирует все значения). Поскольку медиана не учитывает все значения, она гораздо более устойчива к выбросам (в центре "собираются середнячки", а не выбросы).
Процентиль (или перцентиль)
Теперь, когда мы узнали, что такое медиана, мы легко перейдем к процентилю. На самом деле, медиана - это частный случай перцентиля. Перцентиль может быть от 0 до 100 с шагом 1. Медиана - это 50-й перцентиль. Почему 50-й? Потому что это половина.
Обрати внимание, что перцентиль работает с процентом, именно поэтому у нас значения от 0 до 100.
Где нулевой перцентиль означает 0% данных (т.е. самый старт, первый элемент) и 100-ый перцентиль - это 100% данных (т.е. последний элемент). Медиана - это как раз-таки центр данных, а центр - это 50% данных, а раз 50%, то это 50-ый перцентиль.
Посмотри, для медианы мы сделали вот что:
1. Мы отсортировали значения (по возрастанию)
2. Мы нашли середину (которая составляет 50% данных по левой и столько же по правой), в случае с 10 сотрудниками 50% - это 5 сотрудников (что составляет половину от 10), а остальные 50% - это еще 5, верно?
3. Мы вернули значение для нечетного случая или нашли медианное значение (для значений непосредственно перед и непосредственно после).
Обрати внимание, что 50% значений (медиана), имеются в виду 50% от общего количества значений.
В случае с компанией, у нас было 10 сотрудников, получается 50% от 10 (т.е. половина от 10) - это 5. Если у нас 1000 значений, тогда 50% - это 500 и т.д. Запомни, что речь идет про количество значений, которые мы сортируем и затем ищем середину. Можешь об этом думать таким образом. На уроках физкультуры мы выстраивались по росту (помнишь)? В данном случае 50% - это будет ровно половина группы.
Поскольку 50-й процентиль является медианой. Давай закрепим материал на двух простых заданиях.
Задание 1.1
Если 50-ый перцентиль это медиана, то нулевой перцентиль это?
Теперь, когда мы узнали, что такое медиана, мы легко перейдем к процентилю. На самом деле, медиана - это частный случай перцентиля. Перцентиль может быть от 0 до 100 с шагом 1. Медиана - это 50-й перцентиль. Почему 50-й? Потому что это половина.
Обрати внимание, что перцентиль работает с процентом, именно поэтому у нас значения от 0 до 100.
Где нулевой перцентиль означает 0% данных (т.е. самый старт, первый элемент) и 100-ый перцентиль - это 100% данных (т.е. последний элемент). Медиана - это как раз-таки центр данных, а центр - это 50% данных, а раз 50%, то это 50-ый перцентиль.
Посмотри, для медианы мы сделали вот что:
1. Мы отсортировали значения (по возрастанию)
2. Мы нашли середину (которая составляет 50% данных по левой и столько же по правой), в случае с 10 сотрудниками 50% - это 5 сотрудников (что составляет половину от 10), а остальные 50% - это еще 5, верно?
3. Мы вернули значение для нечетного случая или нашли медианное значение (для значений непосредственно перед и непосредственно после).
Обрати внимание, что 50% значений (медиана), имеются в виду 50% от общего количества значений.
В случае с компанией, у нас было 10 сотрудников, получается 50% от 10 (т.е. половина от 10) - это 5. Если у нас 1000 значений, тогда 50% - это 500 и т.д. Запомни, что речь идет про количество значений, которые мы сортируем и затем ищем середину. Можешь об этом думать таким образом. На уроках физкультуры мы выстраивались по росту (помнишь)? В данном случае 50% - это будет ровно половина группы.
Поскольку 50-й процентиль является медианой. Давай закрепим материал на двух простых заданиях.
Задание 1.1
Если 50-ый перцентиль это медиана, то нулевой перцентиль это?
На сервере Jupyter в клубе будет скрытая подсказка и решение. Плюс возможность написать свой код - ответ.
Кстати, мы можем найти минимальное значение таким образом.
Код
np.min(salaries_odd_two)
Результат: 1000
Задание 1.2
Если 50-ый перцентиль это медиана, то сотый перцентиль это?
Если 50-ый перцентиль это медиана, то сотый перцентиль это?
На сервере Jupyter в клубе будет скрытая подсказка и решение. Плюс возможность написать свой код - ответ.
Мы можем найти максимальное значение таким образом.
Код
np.max(salaries_odd_two)
Результат: 41000
Примеры с процентилями
Давай сначала проверим, как согласуется медиана с 50-м процентилем. Сперва проверим на примере четного числа.
Давай сначала проверим, как согласуется медиана с 50-м процентилем. Сперва проверим на примере четного числа.
Код
np.median(salaries_even_two), np.percentile(salaries_even_two, 50)
Результат: (5500.0, 5500.0)
Мы видим, что для четного значения она сходится. Теперь давай еще раз проверим, нет ли нечетного значения.
Код
np.median(salaries_odd_two), np.percentile(salaries_odd_two, 50)
Результат: (5000.0, 5000.0)
Хорошо, как и было обещано, 50-ый процентиль - это медиана. Проверили эмпирически (как говорится, доверяй, но проверяй - очень важное правило при работе с данными).
Теперь мы можем пойти дальше и исследовать более частный случай процентиля (например, 10-й процентиль), но... есть одно но, и нам нужно остановиться на мгновение, чтобы прояснить один момент (потому что иначе сейчас начнут появлятся вопросы).
Помни,
когда мы определяли медиану для четного числа, мы брали среднее значение пары, которая находится непосредственно перед или сразу после середины. Здесь может возникнуть вопрос, а почему именно пара?
Может быть, лучше взять значение непосредственно перед серединой или значение непосредственно после середины или какую-то другую комбинацию, ну вот тут и возникают некоторые проблемы и путаница (где много людей, там всегда много мнений).
Ведь действительно, кто и на каком основании будет это определять? Вероятно, как можно было догадаться, существуют различные определения того, как следует считать процентили, а также существует довольно много различных реализаций (в `numpy`, например, мы реализовали 5 различных версий, ниже есть ссылка на публикацию в которой упоминается 9 возможных версий).
Параметр `interpolation` для функции `np.percentile` как раз и отвечает за выбор способа подсчета. Из имеющихся у нас: `'linear'`, 'lower', 'higher', 'nearest' или 'midpoint'. В файле с бонусом будет объяснение, как именно рассчитывается `linear` (который стоит по умолчанию).
Сейчас, для простоты можно считать, что 10-й процентиль означает следующее:
1. мы сортируем значения по возрастанию
2. мы находим 10 процентов данных (от меньшего до большего, если у нас 2000 значений, то 10% от 2000 это 200, т.е. 200 значение)
3. мы берем значение (пару или комбинации из этой пары, которая находится прямо перед и сразу после)
В случае `linear` формула немного похитрее, но используется именно пара (подробнее найдешь в бонусном уроке).
Теперь мы можем пойти дальше и исследовать более частный случай процентиля (например, 10-й процентиль), но... есть одно но, и нам нужно остановиться на мгновение, чтобы прояснить один момент (потому что иначе сейчас начнут появлятся вопросы).
Помни,
когда мы определяли медиану для четного числа, мы брали среднее значение пары, которая находится непосредственно перед или сразу после середины. Здесь может возникнуть вопрос, а почему именно пара?
Может быть, лучше взять значение непосредственно перед серединой или значение непосредственно после середины или какую-то другую комбинацию, ну вот тут и возникают некоторые проблемы и путаница (где много людей, там всегда много мнений).
Ведь действительно, кто и на каком основании будет это определять? Вероятно, как можно было догадаться, существуют различные определения того, как следует считать процентили, а также существует довольно много различных реализаций (в `numpy`, например, мы реализовали 5 различных версий, ниже есть ссылка на публикацию в которой упоминается 9 возможных версий).
Параметр `interpolation` для функции `np.percentile` как раз и отвечает за выбор способа подсчета. Из имеющихся у нас: `'linear'`, 'lower', 'higher', 'nearest' или 'midpoint'. В файле с бонусом будет объяснение, как именно рассчитывается `linear` (который стоит по умолчанию).
Сейчас, для простоты можно считать, что 10-й процентиль означает следующее:
1. мы сортируем значения по возрастанию
2. мы находим 10 процентов данных (от меньшего до большего, если у нас 2000 значений, то 10% от 2000 это 200, т.е. 200 значение)
3. мы берем значение (пару или комбинации из этой пары, которая находится прямо перед и сразу после)
В случае `linear` формула немного похитрее, но используется именно пара (подробнее найдешь в бонусном уроке).
Код
np.percentile(salaries_even_two, 10)
Результат: 1900.0
В качестве альтернативы можно настроить расчет таким образом, чтобы рассчитывалось точное среднее значение для пары.
Код
np.percentile(salaries_even_two, 10, interpolation="midpoint")
Результат: 1500.0
Код
np.percentile(salaries_even_two, 90, interpolation="midpoint")
Результат: 25000.0

В бонусном уроке найдешь больше объяснений как это считается для разных `interpolation`.
Квартиль
Поскольку у нас есть красивое название для 50-го процентиля (т.е. медианы), вероятно, также должно быть красивое название для 25-го и 75-го (т.е. 1/4 и 3/4). И это действительно так!
У нас есть такое понятие, как квартиль (от лат. quarta — четверть). Всего их три:
- Q1 - 25-й процентиль (или 0,25-квантиль). Это первый или нижний квартиль.
- Q2 - 50-й процентиль (или 0,5-квантиль). Это второй квартиль (обрати внимание, что это медиана).
- Q3 - 75-й процентиль (или 0,75-квантиль). Это третий или верхний квартиль.
Существует еще такое понятие, как квартильный размах (который также называют межквартильным размахом, интерквартильным размахом или квартильным размахом). На английском языке это звучит как Interquartile Range или сокращенно IQR. Это те значения, которые находятся между `Q1` и `Q3` (т.е. 50% значений). В этом случае мы отбрасываем еще 50% (25% до и 25% в конце).
Зачем нам нужен квартиль? В статистике его любят использовать в разных местах, но сейчас он нам нужен хотя бы для того чтобы научиться интерпретировать диаграмму "ящик с усами".
Квартиль
Поскольку у нас есть красивое название для 50-го процентиля (т.е. медианы), вероятно, также должно быть красивое название для 25-го и 75-го (т.е. 1/4 и 3/4). И это действительно так!
У нас есть такое понятие, как квартиль (от лат. quarta — четверть). Всего их три:
- Q1 - 25-й процентиль (или 0,25-квантиль). Это первый или нижний квартиль.
- Q2 - 50-й процентиль (или 0,5-квантиль). Это второй квартиль (обрати внимание, что это медиана).
- Q3 - 75-й процентиль (или 0,75-квантиль). Это третий или верхний квартиль.
Существует еще такое понятие, как квартильный размах (который также называют межквартильным размахом, интерквартильным размахом или квартильным размахом). На английском языке это звучит как Interquartile Range или сокращенно IQR. Это те значения, которые находятся между `Q1` и `Q3` (т.е. 50% значений). В этом случае мы отбрасываем еще 50% (25% до и 25% в конце).
Зачем нам нужен квартиль? В статистике его любят использовать в разных местах, но сейчас он нам нужен хотя бы для того чтобы научиться интерпретировать диаграмму "ящик с усами".
Больше практики
Давай применим полученные знания на примерах. У нас есть таблица в которой есть два столбца: вес и рост (в этот раз людей, не котиков).
Давай сначала загрузим этот набор данных. Используем для этого функцию из библиотеки pandas read_hdf.
Давай применим полученные знания на примерах. У нас есть таблица в которой есть два столбца: вес и рост (в этот раз людей, не котиков).
Давай сначала загрузим этот набор данных. Используем для этого функцию из библиотеки pandas read_hdf.
Код
df_people = pd.read_hdf("../input/height_weight.h5")
df_people.head()
Результат:
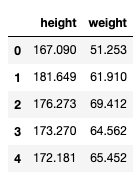
Мы загрузили массив в переменную df_people, который состоит из двух столбцов: рост (height) в сантиментрах и вес (weight) в килограммах.
Давай начнем работать с первым столбцом "рост" вместе, сначала найдем значения:
Давай начнем работать с первым столбцом "рост" вместе, сначала найдем значения:
- минимум
- максимум
- среднее значение
- медиана (Q2 - второй квартиль)
- 25-й процентиль (Q1 - первый квартиль)
- 75-й процентиль (Q3 - третий квартиль)
Код
{
"min": np.min(df_people["height"]),
"max": np.max(df_people["height"]),
"mean": np.mean(df_people["height"]),
"median": np.median(df_people["height"]),
"25-percentile": np.percentile(df_people["height"], 25),
"75-percentile": np.percentile(df_people["height"], 75),
}
Результат:
{'min': 153.10703048706054,
'max': 190.88811584472657,
'mean': 172.70250856571963,
'median': 172.70908012390137,
'25-percentile': 169.42917373657227,
'75-percentile': 175.95331523895263}
{'min': 153.10703048706054,
'max': 190.88811584472657,
'mean': 172.70250856571963,
'median': 172.70908012390137,
'25-percentile': 169.42917373657227,
'75-percentile': 175.95331523895263}
Давай проанализируем полученные нами результаты о росте:
Обрати внимание, что в данном случае среднее и медианное значения практически идентичны.
Предварительно можно считать, что это означает, что у нас нет экстремальных значений (выбросов), которые "испортили" наше среднее значение. Подробнее о нормальном распределении мы поговорим в следующем уроке. Я также обращаю Твое внимание на то, что в данном случае это довольно простой пример, для разминки. Чем дальше, тем интереснее.
Теперь Твоя очередь.
Задание 1.3
Сделай то же самое для веса (т.е. столбец weight). Твоя задача - найти значение: минимум, максимум, среднее, медиану, 25-й процентиль, 75-й процентиль.
- минимум: ~153,11 см.
- максимум: 190,89 см.
- среднее значение: 172.70cm
- медиана: 172,71 см
- 25-й процентиль: 169,43 см
- 75-й процентиль: 175,95 см.
Обрати внимание, что в данном случае среднее и медианное значения практически идентичны.
Предварительно можно считать, что это означает, что у нас нет экстремальных значений (выбросов), которые "испортили" наше среднее значение. Подробнее о нормальном распределении мы поговорим в следующем уроке. Я также обращаю Твое внимание на то, что в данном случае это довольно простой пример, для разминки. Чем дальше, тем интереснее.
Теперь Твоя очередь.
Задание 1.3
Сделай то же самое для веса (т.е. столбец weight). Твоя задача - найти значение: минимум, максимум, среднее, медиану, 25-й процентиль, 75-й процентиль.
На сервере Jupyter в клубе будет скрытая подсказка и решение. Плюс возможность написать свой код - ответ.
Подскажу одну функцию, которая доступна в библиотеке pandas .describe(). Давай сначала применим ее, а затем попытаемся его интерпретировать (так как дети познают мир, сразу все пробуя).
Код
df_people.describe()
Результат:
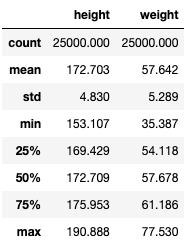
У меня есть хорошая новость для Тебя - таблицу, которая получилась, сможешь самостоятельно интерпретировать.
В результате мы получили таблицу из двух столбцов (для роста и веса) и параметров в строках.
Недвижимость в Польше
Давай посмотрим еще один набор данных, основанный на реальных данных.
В результате мы получили таблицу из двух столбцов (для роста и веса) и параметров в строках.
- count - количество строк (в данном случае у нас 25000 строк в исходном массиве)
- mean - среднее значение
- std - об этом узнаешь в следующем уроке
- min - минимальное значение
- 25% - 25-й процентиль
- 50% - 50-й процентиль (медиана)
- 75% - 75-й процентиль
- max - максимальное значение
Недвижимость в Польше
Давай посмотрим еще один набор данных, основанный на реальных данных.
Код
df_property = pd.read_hdf("../input/property.h5")
df_property.head()
Результат:
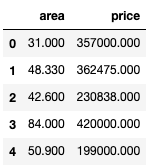
В данном случае у нас есть массив с двумя столбцами: площадь объекта (area) в м2 и цена объекта (price) в злотых (недвижимость в Польше). Давай начнем изучение этого набора с того, что уже успели изучить.
Задание 1.4
Твоя задача - начать анализировать два столбца (area и price) найти:
Твоя задача - начать анализировать два столбца (area и price) найти:
- среднее значение
- минимальное значение
- 25-й процентиль
- 50-й процентиль (медиана)
- 75-й процентиль
- максимальное значение
На сервере Jupyter в клубе будет скрытая подсказка и решение. Плюс возможность написать свой код - ответ.
Резюме
В этом уроке мы узнали:
В этом уроке мы узнали:
- - что есть среднее (арифметическое) значение
- - среднее значение очень чувствительно к выбросам, поэтому можно быстро сделать неверные выводы. Вспомни компанию, в которой было 9 сотрудников, зарабатывающих 1000 евро, и один человек (большой босс), зарабатывающий 41 000 евро. Средняя зарплата в этой компании составляет 5000 EUR, что в 5 раз больше, чем у 9 из 10 сотрудников :)
- - средний показатель по стране (например средняя зарплата) - измеряется как среднее значение, с одной стороны, возможно, потому что это легко понять (большинству), но, вероятно, также потому, что оно может "завысить" или "занизить" фактическое состояние
- - также помни про аналогию - "средняя температура по больнице" (это своего рода избитая фраза среди аналитиков, что смотрим на что-то, что не имеет смысла и нужно копать глубже).
- - медиана рассчитывается иначе, чем среднее значение и более устойчива к выбросам (выбросы, как помнишь - это экстремально завышенные или заниженные значения), так как учитывают только центральное значение (или среднее двух значений - "центральной пара", расположенной непосредственно перед серединой и после середины)
- - медиана (а также квартиль) является частным случаем процентиля
- - нулевой процентиль - минимальное значение, 100-й процентиль - максимальное значение, 25-й процентиль - первый квартиль, 50-й процентиль - второй квартиль (и она же медиана), 75-й процентиль - третий квартиль.
- В этом уроке мы рассмотрели все показатели из функции `.describe()`, кроме стандартного отклонения (`std`). Стандартное отклонение, а также вариация, нормальное распределение, почти три сигмы, распределение с длинным хвостом, нормализация этих распределений будут рассмотрены в следующем уроке (плюс будут и другие полезности). Приглашаю!
Это был пример первого урока из курса "Практическое введение в статистику". Всего в курсе 15 уроков + бонусные задания.
Как видишь, изучать статистику можно без сложных и запутанных формул. Получить доступ к курсу можно став участником клуба.
Присоединяйся сейчас и начни свое комфортное обучение.
Как видишь, изучать статистику можно без сложных и запутанных формул. Получить доступ к курсу можно став участником клуба.
Присоединяйся сейчас и начни свое комфортное обучение.
Недавно в телеграм я задавал такой вопрос:
Когда смотришь прогноз погоды и видишь: вероятность, что завтра будет дождь - 55%, как Ты это интерпретируешь? :)
Большинство людей выбрали ответы 2 или 3, и оба случая неправильные! Почему? Потому что в этой жизни 100% гарантий не может быть ни на что (кроме смерти и налогов).
Тот факт, что мы имеем вероятность 55%, вовсе не гарантирует, что дождь пойдет в 55 случаях из 100. Дождь может пойти только в 45 случаях из 100 - не веришь? Очень хорошо! Давай проверим. Просто клонировать 100 вселенных мы не можем, но давай попробуем сделать это другим способом - напишем простой код на Python.
На диаграмме ниже представлена симуляция из 100 экспериментов. В каждом эксперименте мы заранее задаем вероятность 55% и проверяем, сколько раз из 100 дней действительно пойдет дождь. И мы проводим такой эксперимент 100 раз.
Когда смотришь прогноз погоды и видишь: вероятность, что завтра будет дождь - 55%, как Ты это интерпретируешь? :)
- Завтра на 55% площади будет 100% дождь, на 45% - не 100%?
- Если проверить 100 ситуаций, то 55 раз дождь действительно шел на 100%, а 45 раз - на 0% (т.е. дождь не шел на 100%).
- Если бы у нас было 100 клонов нашей вселенной, то в 55 из них дождь шел на 100%, в 45% - на 0%.
- Не знаю, но завтра я возьму с собой зонтик
- Я не знаю, но я хочу знать, что все это значит
Большинство людей выбрали ответы 2 или 3, и оба случая неправильные! Почему? Потому что в этой жизни 100% гарантий не может быть ни на что (кроме смерти и налогов).
Тот факт, что мы имеем вероятность 55%, вовсе не гарантирует, что дождь пойдет в 55 случаях из 100. Дождь может пойти только в 45 случаях из 100 - не веришь? Очень хорошо! Давай проверим. Просто клонировать 100 вселенных мы не можем, но давай попробуем сделать это другим способом - напишем простой код на Python.
На диаграмме ниже представлена симуляция из 100 экспериментов. В каждом эксперименте мы заранее задаем вероятность 55% и проверяем, сколько раз из 100 дней действительно пойдет дождь. И мы проводим такой эксперимент 100 раз.

Как можно видеть, только для 4% (в 4 экспериментах из 100) дождь действительно шел целых 55 раз, но были и случаи, когда дождь шел только в 45 случаях из 100 или в 66 случаях из 100. Значения меняются, и как теперь с этим справиться?
Давай погрузимся немного глубже и попытаемся лучше понять природу случайностей. Ниже приведен график. Посмотри сразу и будем интерпретировать его вместе :)
Давай погрузимся немного глубже и попытаемся лучше понять природу случайностей. Ниже приведен график. Посмотри сразу и будем интерпретировать его вместе :)

Метод Монте-Карло - Будет ли дождь?
Есть метод Монте-Карло, который позволяет моделировать достаточно сложные вещи, даже те, которые сложно решить аналитически. Давай воспользуемся этим методом и посмотрим, как часто возникает вероятность в нашей задаче/вопросе.
Красная линия составляет 55%, и, как можно увидеть, синяя линия только начинает сходиться со временем. Что на практике означает именно то, что подразумевается под случайностью. Интересно, что такие симуляции тоже выглядят каждый раз по-разному, но есть и общая часть — через какое-то время шансы действительно начинают сходиться.
Что это значит для Тебя? Ни на что нет 100% гарантий, помни об этом. Даже если у нас "честная" монета, у нас есть 50% вероятность выпадения орла и 50% вероятность выпадения решки, но... может случиться так, что подбросив монету, получим орла (или решку) 10 раз подряд - такое не очень часто бывает, но исключать нельзя.
Все вышеперечисленное и многое другое есть в авторском курсе "Практическое введение в статистику" (на языке Python).
Будет много практических экспериментов, чтобы лучше закрепить знания и наконец понять, каково это - работать со статистикой на практике, а не только в книгах. Чтобы понять и использовать эти знания, не обязательно иметь "научную" степень.
- У нас есть два сценария: будет дождь или нет (т.е. два возможных варианта).
- Проведем 100 экспериментов (на графике это отмечено как 'n'), допустим, что у нас есть 100 прогнозов, что будет дождь с вероятностью 55%, и мы знаем, как это было на самом деле.
- Прибавляем математическое ожидание шанса (сверху было 55%).
Красная линия составляет 55%, и, как можно увидеть, синяя линия только начинает сходиться со временем. Что на практике означает именно то, что подразумевается под случайностью. Интересно, что такие симуляции тоже выглядят каждый раз по-разному, но есть и общая часть — через какое-то время шансы действительно начинают сходиться.
Что это значит для Тебя? Ни на что нет 100% гарантий, помни об этом. Даже если у нас "честная" монета, у нас есть 50% вероятность выпадения орла и 50% вероятность выпадения решки, но... может случиться так, что подбросив монету, получим орла (или решку) 10 раз подряд - такое не очень часто бывает, но исключать нельзя.
Все вышеперечисленное и многое другое есть в авторском курсе "Практическое введение в статистику" (на языке Python).
- Начинается 14 ноября 2022 года
- Длится 3 недели (3 модуля)
- 15 практических уроков + отдельное пошаговое видео для каждого из них + бонусные уроки + домашние задания
- Практические знания, которые помогут извлечь ценность из данных
Будет много практических экспериментов, чтобы лучше закрепить знания и наконец понять, каково это - работать со статистикой на практике, а не только в книгах. Чтобы понять и использовать эти знания, не обязательно иметь "научную" степень.